
������ͼ���� ��С��
�����ڹ���Ա�����У�“�������”�����“�г�����”һ�����ǹ������Ϊͷʹ�����ͣ�Ҳ���������꿼�Եıؿ��ص����͡����֮������Ϊ�������������ԭ�������㣺(1)����֪ʶ�����������Ϊ���ֿ����ԴӸ��б�ҵ֮�ͺ����ٽӴ�������ϵ�֪ʶ��������Ӧ��ʱ�ͻ���ú�İ������֪�Ӻ����֡�(2)����ģ�͵IJ���Ϥ�����Խ������ڱ���ʱ��Ҫ�������������֡����ڻ���֪ʶ���֣������Ҫ��������ԭ�����ӷ��ͳ˷�ԭ��;����������к����;������ʽ�����й�ʽ����Ϲ�ʽ������ʽ���Գ������ͣ��ܽ���Ҫ��������ģ�ͩp��λ����ģ�ͩp�Ͳ��ģ�͵ȡ������Ͼ����������ҽ��ܡ�
����һ��������ģ��
����(1)����ģ��
�����������������Ҫ����һ������ڵ����⡣����˼·��Ϊ����
������һ������Ҫ����һ��(������)������������������һ�����壬��������
������һ������;
�����ڶ����������������������ɽ⣬����Щ��������������������С�
������շ������������Ҫ���ڲ�һ������ڵ����⡣����˼·��Ϊ����
������һ����������Ҫ����һ��(������)�����壬ֻ����������Ҫ�����
������;
�����ڶ���������Ҫ�������������ź�˳����������γɵĿ�϶�С�
����(2)��������
����������ij�����8ǹ������4ǹ��ǡ��3ǹ�������ϵ������ж�����?( )
����A.720 B.480 C.224 D.20
��������������ĿҪ����ϵ���ǹ�У�ǡ��3ǹ�������ϣ�����˵4ǹ�У�3ǹ����һ��
����ʣ���1ǹҪ����3ǹ����һ�𡣸������������յ�ģ�ͣ���һ���3ǹ
����ʹ����������������������1������;����1ǹ������ǰ��3ǹ������
�������Dz�ա��Ƚ�δ���ϵ�4ǹ���У��γ�5����;�ٽ�����“3”ǹ�Ͷ���“1”
����ǹ�������е�2�����У�����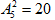 (��)���Σ��ʴ���D.
(��)���Σ��ʴ���D.
����������λ����ģ��
����(1)����ģ��
������N���ź�N���ŷ⣬ÿ���Ŷ���װ���Լ����ŷ�����ܵķ�����������Ϊ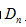 ����
����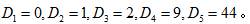
������
����(2)��������
����������(�㽭2011-50)��λ��ʦ�۲�ʱ������һ�����ֲˡ�����Ҫ��ÿ��ȥƷ��һ��
�����ˣ������ܳ��Լ������ǵ��ˡ��ʹ��м��ֲ�ͬ�ij���?( )
����A.6�� B.9�� C.12�� D.15��
����������������ܶ����ѡ��ö�ٷ����⣬���ǻỨ��һ����ʱ�䡣����ֱ��Ӧ�ô�λ
�������Ź�ʽ���ĸ��˵Ĵ�λ���Ŷ�Ӧ9�֡��ʴ�ΪB��
�����������ģ��
����(1)����ģ��
������M����ͬ�Ķ����ָ�N���ˣ�ÿ�����ٷ�һ������һ����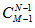 �ֲ�ͬ�ķַ���
�ֲ�ͬ�ķַ���
����(������Ҫʹÿ�����ٷ�һ���Ļ����൱�ڽ�M�������ֳ�N�ѣ���ʱֻ��Ҫ��M����
����ͬ�Ķ���֮���N-1���塣)
����(2)��������
��������1��(����2010-46)ij��λ������30��ѧϰ���Ϸ��Ÿ�3�����ţ�ÿһ����
���������ٷ���9�ݲ��ϡ���һ���ж����ֲ�ͬ�ķ��ŷ���?( )
����A.12 B.10 C.9 D.7
���������������ó�24�ݲ���ÿ�����ŷ�8�ݣ���ʱ���“6�ݲ��Ϸ���3�����ţ�
����ÿ���������ٷ�1��”�����Dz��Ļ���ģ�ͣ��������ò�巨����5����
�����в���2���壺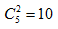 (��)���ʴ�ΪB
(��)���ʴ�ΪB
��������2����6����ͬ��ƻ���ָ�3��С���ѣ�����һ���ж����ַ��䷽��?( )
����A.16 B.20 C.24 D.28
����������������ÿһ��С����“��”һ��ƻ������ô�����ܹ���6+3=9 (��)ƻ
����������ʱ�����ת��Ϊ“��9��ƻ�������3��С���ѣ�Ϊ�˳���֮ǰ���ƻ����
����Ҫ�����ڷ����ʱ��ÿ��С�������ٵõ�1��ƻ��”�����ò�巨������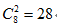 (��)�ַ���
(��)�ַ���
���༭�����ݻ�ͼ��
