
����
�����غ���ʵ��
������ʵ���ߡ�Ƥ�ǽ�
������ʵ����̡�
����ʵ��һ��Һ���غ�
�������ͯ��������һģһ���ı��ӣ�����������װ����ͬ������Һ�塣�ڶ�ͯ��Ϊ��������װ����ͬ������Һ���һ�������е�Һ�嵹��һ���Ƚϸߵ��Ƚ���С�ı�������ʶ�ͯ��“�������(�ϸߵ�һ��)���ˮ���������(�Ƚϰ��ı���)��ˮһ���ࡢ���ٻ��ǽ϶�?”


����ʵ����������غ�
����ʵ���У������ͯ��������һģһ����Ŧ�ۣ��ڶ�ͯȷ������Ŧ�۵�������һ����֮�����е�һ��Ŧ�۵ļ������������ѹ�����ʶ�ͯ�����ŵ�Ŧ�����Ƿ���ͬ?
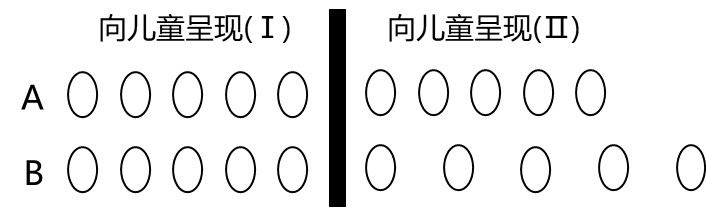

����ʵ�����������غ�
�����ڶ�ͯ��ǰ���ų�������ͬ����ľ�����ڶ�ͯ��������ľ��������Ⱥ�����һ������(������)�ƶ�һ�ξ��룬�ʶ�ͯ����ľ���ij����Ƿ����?


����ʵ���ģ������غ�
�������ͯ����������ͬ��Բ���࣬Ȼ���Ŷ�ͯ���潫���е�һ��Բ����ѹ����Բ�Σ��ʶ�ͯԲ�εĺ���Բ�ε��ĸ���Ƥ���?


������ʵ������
����ʵ��һ��6��7�����µĶ�ͯ�����ݱ�����ˮ�ĸ߶�ȥ�ж�ˮ�Ķ��٣��������DZ��ӵĿھ��Ĵ�С����6��7�����ϵĶ�ͯ���������һ�㶼��������ȷ�Ļش𣬼����Ƕ�ͬʱ����ˮ��ĸ߶Ⱥͱ��ӿھ�����ά��������������ˮ�Ķ��١�
����ʵ�����5��6���ͯ��ʱ���ݳ����ж϶��٣���ʱ����ܶ��ж϶��٣�����δ�ﵽ�غ㡣ֱ��8�����ҵĶ�ͯ���ܸ���һһ��Ӧ�Ĺ�ϵ��������֪����״�ı��Ӱ�죬�ﵽ�����غ㡣
����ʵ������Լ8���Ժ�Ķ�ͯ�Ѳ���֪����״��Ӱ�죬�ش�����С������һ��������С�Ķ�ͯ��֪����״�ı��Ӱ�죬��˵����İ�������ij�������İ�������ij���
����ʵ���ģ�7����ǰ�Ķ�ͯ���е���ΪԲ�ε���Ƥ��࣬�е���Ϊ��Բ�ε���Ƥ��ࡣ��7��8�����ϵĶ�ͯ����Ϊ��������һ���ࡣ
������ʵ����ۡ�Ƥ�ǽ���Ϊһ����8����������غ�ĸ���(����������̬��α仯���䱾�����Բ���)����־�Ŷ�ͯ�����������Σ��Ƕ�ͯ��֪��չ�е�һ���ʵķ�Ծ�������������Ƥ�ǽ��������֪��չ��֮һ��Լ7—11������Ρ������������˼ά�ĺ��ĸ������ͯ�Ķ�����չ����������ʱ������˼ά����������˿������ص㣬���������뻥���ԣ���ʼ�������������ȡ�������������ݻ����غ�����ʱ��ͯ�ܴ�����ľ���仯��ץס����ı��ʡ�
����������ʾ����
����1.����ѡ������ΪС�ں�С��ե��������ͬ�������ʹ�֭���ֱ�װ�ڴ�С��ͬ�������������������С�����ã�С��˵��“��Ҫ�Ɑ���”��С�����Ա�˵“��ʵ������һ�����”�����������õĻش𣬿����жϳ�С�ں�С��ֱ���( )��
����A.��֪�˶��κ�ǰ����� B.ǰ����κ;��������
����C.��������κ���ʽ����� D.��֪�˶��κ;��������
����1.���𰸡�B
���������������⿼�����Ƥ�ǽܵ���֪��չ�����ۡ�Ƥ�ǽܽ��˵�������չ��Ϊ4���Σ���֪�˶��Ρ�ǰ����Ρ�����������Լ���ʽ����Σ�����ǰ����εĶ�ͯû�л���غ�ĸ������������ζ�ͯ���Ѿ��������غ�ĸ���������������С��δ����غ�����С�������غ�������С�ڴ���ǰ����Σ�С�촦�ھ�������Ρ��ʱ���ѡB��
����2.����ѡ������Ƥ�ǽܵ���֪��չ�����ۣ���ʼ����غ����Ķ�ͯ����˼ά��չ����( )��
����A.��֪�˶��� B.ǰ�����
����C.��������� D.��ʽ�����
����2.���𰸡�C
���������������⿼�����Ƥ�ǽܵ���֪��չ�����ۡ�����Ƥ�ǽܵ���֪��չ�����ۣ���������ζ�ͯ���ص��У�(1)�����˳�����˼ά������ת���ܹ�����������;(2)����˳��ȡ����������������ȷ�����غ��ϵ;(3)��ά˼ά;(4)ȥ��������;(5)������˼ά���ʱ���ѡC��
����3.����ѡ����ͬ��һ����Ƥ�࣬�ӽ�����״��ɰ�ʡ�����Ϊ��ʹ�õ���Ƥ����ڰ�ʣ���˵������δ����( )�ĸ��
����A.�������� B.������
����C.�غ� D.˼ά����
����3.���𰸡�C
���������������⿼�����Ƥ�ǽܵ���֪��չ�����ۡ�Ƥ�ǽܽ��˵�������չ��Ϊ4���Σ���֪�˶��Ρ�ǰ����Ρ�����������Լ���ʽ����Ρ����У�ǰ����εĶ�ͯû�л���غ�ĸ����ν�غ���ָ�������ﲻ����������̬��α仯�������������Բ��䡣�����������������δ��������غ㡣�ʱ���ѡC��
��������ʦ�ʸ�ͼ���Ƽ�

���༭��liyulu��
