该公告已过公示时间，对该公告内容进行下架处理，给您带来的不便敬请谅解。
【试题练习】
某地突发疫情，需要全员核酸检测。一单位派出两个志愿者小队帮忙辖区内5个社区维持核检秩序。要求每个志愿者小队至少帮助2个社区，且每个社区只能由其中一个志愿者小组帮忙。若任务分配完全随机，则梧桐小区和霞光小区核检秩序由同一个志愿者小队帮忙维持的概率为：
A.45%以上
B.35%到45%
C.25%到35%
D.25%以下
正确答案：B
【解析】第一步，本题考查概率问题，属于基本概率。
第二步，两个志愿者小队分别要帮忙2个社区和3个社区，帮忙维持秩序的方式共有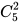
×
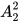=20种。满足两个小区由同一个志愿者小队帮忙的情况为两种：（1）均在负责2个社区的志愿者小队，则有
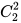=1（种）；（2）均在负责3个社区的志愿者小队，则有
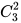=3（种），共有1+3=4种。又因两个志愿者小队分别要帮忙2个社区和3个社区有不同顺序，则共有4×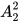=8（种）。
第三步，梧桐小区和霞光小区核检秩序由同一个志愿者小队帮忙维持的概率为
=40%。
因此，选择B选项。
（编辑：luxianyue）
