
����
����������ϵ֪ʶ����⼼��

�������в⿼���У��ֿ�����ͷʹ�ľ���������ϵ���Լ۱����岻��̫�ߣ���Ҳ����Ϊ�������ص�����Ҳ�ܳ�Ϊ���������Ĺؼ���顣������ϵ�е��г������������һ���������ֱ�Ӵ��빫ʽ�����ݽ��м��㣬���Ǵ����ͻ���Ҫ����һ�㣬�漰�������������е�ʱ������һ��ҡ����ԣ�����С�����ҽ���һ�ֿ��ٽ���г����������ι�����ֻ��·����������Ľ��⼼��——��ʽ�ھ�����
������������
�������ڴ����������͵��ص����������β������θ�������ʱ���������ľ��룬�������·�̵����⡣����������������Ǿ��벻ͬ������ľ��룬��S=3S1-S2(S1��������һ�ξ���A��ľ���;S2�������ڶ��ξ���B��ľ���);������������������Ǿ���ͬһ��ľ��룬��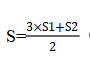 (S1��������һ�ξ���A��ľ���;S2�������ڶ��ξ���A��ľ���)��
(S1��������һ�ξ���A��ľ���;S2�������ڶ��ξ���A��ľ���)��
�����������⽲��
������1.����A�ɼ׳ǿ����ҳǣ�����B���ҳǿ����׳ǣ�����ͬʱ�������Ը��Ժ㶨���ٶ���ʻ����;�е�һ������ʱ��������׳�Ϊ35ǧ�ס����������������ԭ�����ٶ���ʻ��Ŀ�ĵس��к������۷���;����һ����������ʱ�������ҳ�Ϊ25ǧ�ס�������������( )ǧ�ס�
����A.80 B.85 C.90 D.95

�������𰸡�A��������������ȷ�����ֱ�ʾ���������ε��г������⣬���Ҹ�����һ��������׳Ǻ͵ڶ����������ҳǵľ��룬�Ƿ������������Ǿ��벻ͬ������Ĺ�ʽ��S=3S1-S2=335-25=80ǧ�ף��ʼ������ǵľ���Ϊ80ǧ�ף�����ѡ��A��
������2.�������˷ֱ��A��B����ͬʱ��������Զ��У������ǵ�һ������ʱ�����B�����104�ף�Ȼ�����˼�����ǰ�ߣ�������Ŀ�ĵغ��������أ����ڶ�������ʱ������B�صľ���Ϊ40�ס���AB���صľ����Ƕ���?
����A.124�� B.144�� C.168�� D.176��
�������𰸡�D��������������ȷ������Զ��У����ҷֱ����������������B�صľ��룬����ʹ��������������ͬһ�ص�Ĺ�ʽ���㣺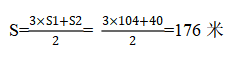 ����AB���صľ���Ϊ176�ף�����ѡ��D��
����AB���صľ���Ϊ176�ף�����ѡ��D��
����ͨ������������Ŀ��ʾ�������Ÿ�λ�������ڴ������͵Ľ���˼·���˸���һ������ʶ�����ڴ���ڱ����Ĺ����У��������Ƶ���Ŀ������ֱ������������ʽ�����ɽ⣬��Ȼ���ڴ��ڵ�����������֪����һ��������ã��ܹ��ܴ�̶�������Լ��������ٶȡ�
���༭��liyulu��
