模块四 数字推理
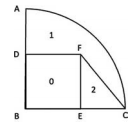
6. 某疫苗共需接种 2 剂次方可达到最佳效果。 A 市的接种人数占比统计如右图所示, 其中, 区域 “0” 表示尚未接种, 区域 “1” 表示只接种 1 剂次, 区域 “2” 表示已接种 2 剂次。 假设 ABC 是四分之一圆面, D、 E 是中点, BDFE 是正方形, 则该市某疫苗只接种 1 剂次的人数占比:
A. 超过 40%但不到 50%
B. 刚好 50%
C. 超过 50%但不到 60%
D. 超过 60%
7. 南部某战区一个 10 人小分队里有 6 人是特种兵, 某次突击任务需派出 5 人参战, 若抽到 3 名或 3 名以上特种兵可成功完成突击任务, 那么成功完成突击任务的概率有多大?

8. 张、 王、 刘、 李、 陈五人按照特定的规则随机分配给 A、 B、 C、 D 四个任务组,要求每组至少分配 1 人, 张不分配在 A 组, 李必须分配在 C 组, D 组只分配 1 人。 问张和王分配在同一组的概率为:
A. 不到 5%
B. 5% ~10%之间
C. 10% ~15%之间
D. 超过 15%
9. 植树节期间, 某单位购进一批树苗, 在林场工人的指导下组织员工植树造林。假设植树的成活率为 80%, 那么, 该单位职工小张种植 3 棵树苗, 至少成活 2 棵的概率是:

10. 物业派出小王、 小曾、 小郭三名工作人员负责修剪小区内的 6 棵树, 每名工作人员至少修剪 1 棵 (只考虑修剪的棵数), 问小王至少修剪 3 棵的概率为:

11. 甲、 乙两个箱子中分别装有不同数量的某种商品, 总数不到 100 件, 如果从甲或乙箱子中随机拿出 1 件这种商品, 拿到次品的概率分别为 5%和 10%。 如果将两箱内的商品混合后再随机拿出 1 件, 则拿到次品的概率为 6%。 问从乙箱中随机拿出 3 件这种商品, 均不为次品的概率 x 在以下哪个范围内?
A. x<72%
B. 72%≤x<81%
C. 81%≤x<90%
D. x≥90%
次后, 任一张卡片正面向上的概率为:
A. 72. 25%
B. 74. 5%
C. 82. 5%
D. 85%
扫码【添加客服】即可领取华图参考答案



